平均律では各音の間隔が一定で、\(440Hz\)から1オクターブ分の各音の周波数は
\begin{align}
f=440 \times 2^{i/12}(i =0 \sim11)
\end{align}
で与えられる。また正弦波は
\begin{align}
f=\sin \omega t
\end{align}
であるので、この式を使い和音の波形を合成する。
ドミソの波形は
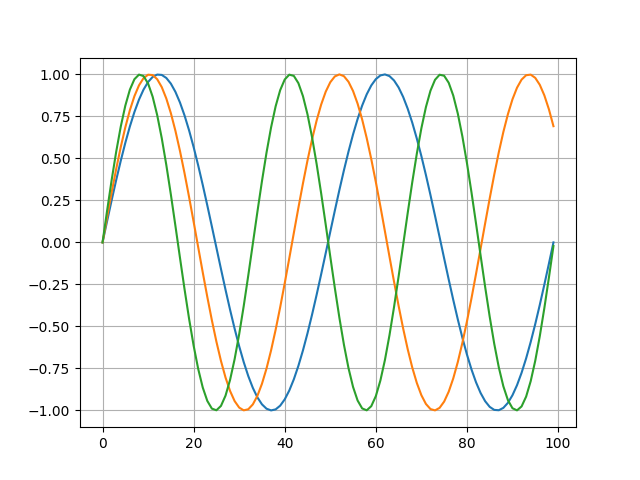
これを合成すると
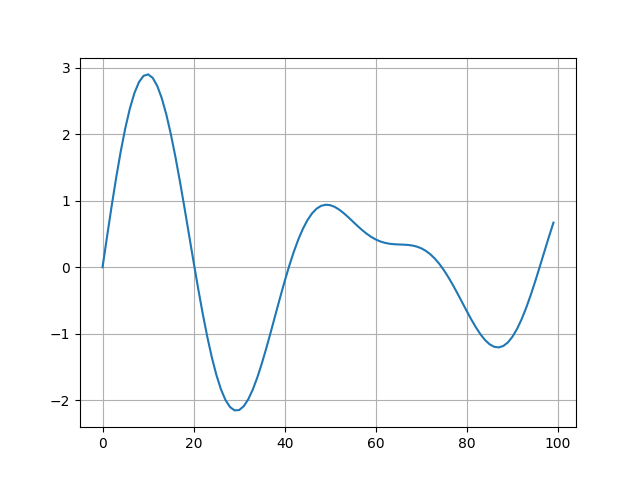
以下ソースコード
import numpy as np
from matplotlib import pyplot as plt
N=100
f0 = 27.5
t = 2/f0
A = 2**(0/12)
Asharp = 2**(1/12)
B = 2**(2/12)
C = 2**(3/12)
Csharp = 2**(4/12)
D = 2**(5/12)
Dsharp = 2**(6/12)
E = 2**(7/12)
F = 2**(8/12)
Fsharp = 2**(9/12)
G = 2**(10/12)
Gsharp = 2**(11/12)
print(f0*A)
print(f0*G)
omega_t_A = 2 * np.pi * f0 * A * np.linspace(0, t,N)
omega_t_C = 2 * np.pi * f0 * C * np.linspace(0, t,N)
omega_t_E = 2 * np.pi * f0 * E * np.linspace(0, t,N)
fa = np.sin(omega_t_A)
fc = np.sin(omega_t_C)
fe = np.sin(omega_t_E)
f = fa+fc+fe
plt.figure()
plt.plot(f)
plt.grid(True)
plt.figure()
plt.plot(fa)
plt.plot(fc)
plt.plot(fe)
plt.grid(True)
plt.show()


コメント